By Ruth Beck, Dwayne Beck, Sara Berg and David Karki
In this information age, farmers may find it challenging to identify trustable sources. There are many companies trying to sell products attached to claims that may or may not be true. It is important for farmers to find a path through the hype and be able to determine if a product will benefit them or not.
Statistical analysis is one way to separate fact from fiction.
Statistical Analysis in Agriculture
Statistical analysis can be used to test the likelihood that new methods, products or varieties are truly different under the conditions tested, or whether the differences were just by chance. If you test only one comparison (i.e. applying one treatment to half of the field and another to the other half) it is impossible to tell if the differences (if any) will be repeatable if the test was performed again. This is like trying to determine if your neighbor has heavier cows than you do by weighing just one cow. The best solution would be to weigh all the cows, which obviously requires much more work.
Application
Statistical analysis is useful because it considers that most natural systems have a “normal” distribution. In a normally distributed population (or sample) half of the individual observations are greater than the average (mean) and half are less, with much of the observations aggregated around the mean.
Standard deviation is a measure of the amount of variability of the observations from the calculated mean. It is desirable that 34% of observations fall within one standard deviation below the mean, and another 34% one standard deviation above.
Ideally, 14% of the observations will fall 1-2 standard deviations above the mean and another fourteen percent 1-2 standard deviations below; the remaining observations fall outside of this range. In the example above, the probability of making the correct decision increases with the number of cows weighed because you have a better estimate of the mean and the standard deviation of the herd.
Once a representative sample of cows are weighed in each herd, it is possible to develop a rough estimate of the average weight and the likely range of weights in the herd. Some herds will have a large difference between the largest and smallest cows, resulting in a larger standard deviation than herds that have been selected to have less difference.
SDSU Extension Research: Statistical analysis
Methods
Researchers at SDSU use similar statistical analysis techniques to evaluate agronomic experiments. If you had a perfectly uniform field planted to a crop that is treated uniformly, and you weighed each strip from the field as it was harvested, the numbers would differ (like the cow weights differed). You could calculate the mean and standard deviation of this random (natural) variation. This is why replication of treatments is important within research trials, to limit the variability with the “check” or standard control treatment.
By adding one strip of a different variety you could not be sure if it was better or worse than the check, no matter what it was, because you have only one strip. If it was outside the range of two standard deviations above or below the mean of the check, you still would not be sure because two percent of observations fall into that category.
On the other hand, if you had 4-10 strips of the new variety in the field and they all fell within 1-2 standard deviations of the mean; there is now statistical evidence that this variety is either better or worse than the check.
 Much of small plot and field scale research is set up the same way. A check treatment is identified; it is put into the trial a number of times to allow the researcher to determine what the mean and standard deviation would be for the field. Other treatments are added and each are repeated the same number of times.
Much of small plot and field scale research is set up the same way. A check treatment is identified; it is put into the trial a number of times to allow the researcher to determine what the mean and standard deviation would be for the field. Other treatments are added and each are repeated the same number of times.
These are arranged randomly to avoid any bias that might happen due to location within the field. Care is taken to assure the trial is conducted in an area as uniform as possible. After the research is completed, all the data (yield, moisture, plant nutrient content, etc.) is analyzed to determine each treatment’s mean and standard deviation. This allows us to compare the treatments to the check and to each other.
Determining Significance
When research is presented, it is common for the treatment averages (means) to be listed followed by a letter. The bottom of the table states: “Means followed by the same letter are not different at the 0.05 level of significance”.
This means that at the 0.05 level of significance, if they have different letters (a, b, or c) that there is a 95% chance that the treatments are different (5 percent chance they are the same) under the conditions in this trial. If the 0.01 level of significance is used, the chance that treatments are different increases to 99%.
This seems like a very stringent approach but in general, it is better to have a producer continue to use an established variety than switch to a newly introduced variety (or technique) that is no better because added costs are involved.
In variety trials, you will commonly see a star or something similar with the note that these varieties or hybrids were in the top yielding group. This also identifies statistical significance, simply expressed in a different way.
Coefficient of Variation
The other note you may (or should) see on a research report is ‘CV’. This stands for ‘coefficient of variation’. This is a measure of how uniform the study was in terms of the performance of the same treatment over the different replications (or locations) in the trial.
If this number is high, there may have been in-field variability due to stand or weed issues, severe lack of uniformity in the test area, insect damage that was not uniform, spray drift, or unpredictable weather issues. Trials with a high CV should be viewed with great caution.
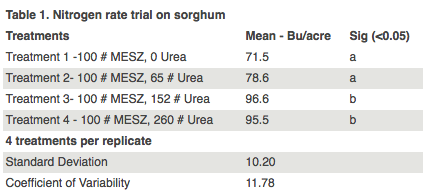
Example Results: Nitrogen rate trial on sorghum
The table below shows the results of a nitrogen rate trial on sorghum. Each strip was replicated four times over the field. Yields listed are the mean yields of four treatments as the experiment was replicated four times.
The letters in the third column indicate that treatment 1 and 2 are significantly different from treatment 3 and 4, 95 percent of the time.
However, treatments 1 and 2 are not significantly different from each other and treatments 3 and 4 are not significantly different from each other.
In Summary
We hope that this explanation will help farmers and others evaluate research.
If a claim is made that one variety out yielded another, one can ask “Were treatments replicated in this research?” and “Do yield results represent the mean across replications?” Other questions might include “What was the least significant difference between treatments?” and lastly “What was the CV for the trial?”
Errors can happen in any experiment but when accepted procedures are in place, research results can provide valuable, applicable information. Procedures and protocols do make a difference.





